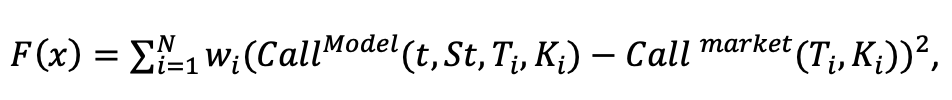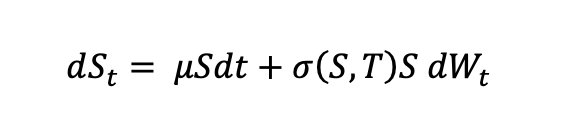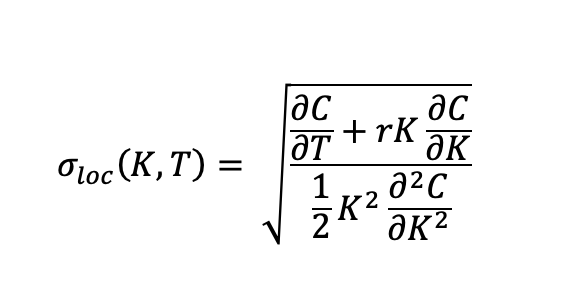UnRısk: Challenges in Dupire Model Calibration

Valuation of Equity FX Instruments

14. August 2024

UnRısk News: Latest Highlights and Innovations

21. August 2024

Challenges in Dupire Model Calibration

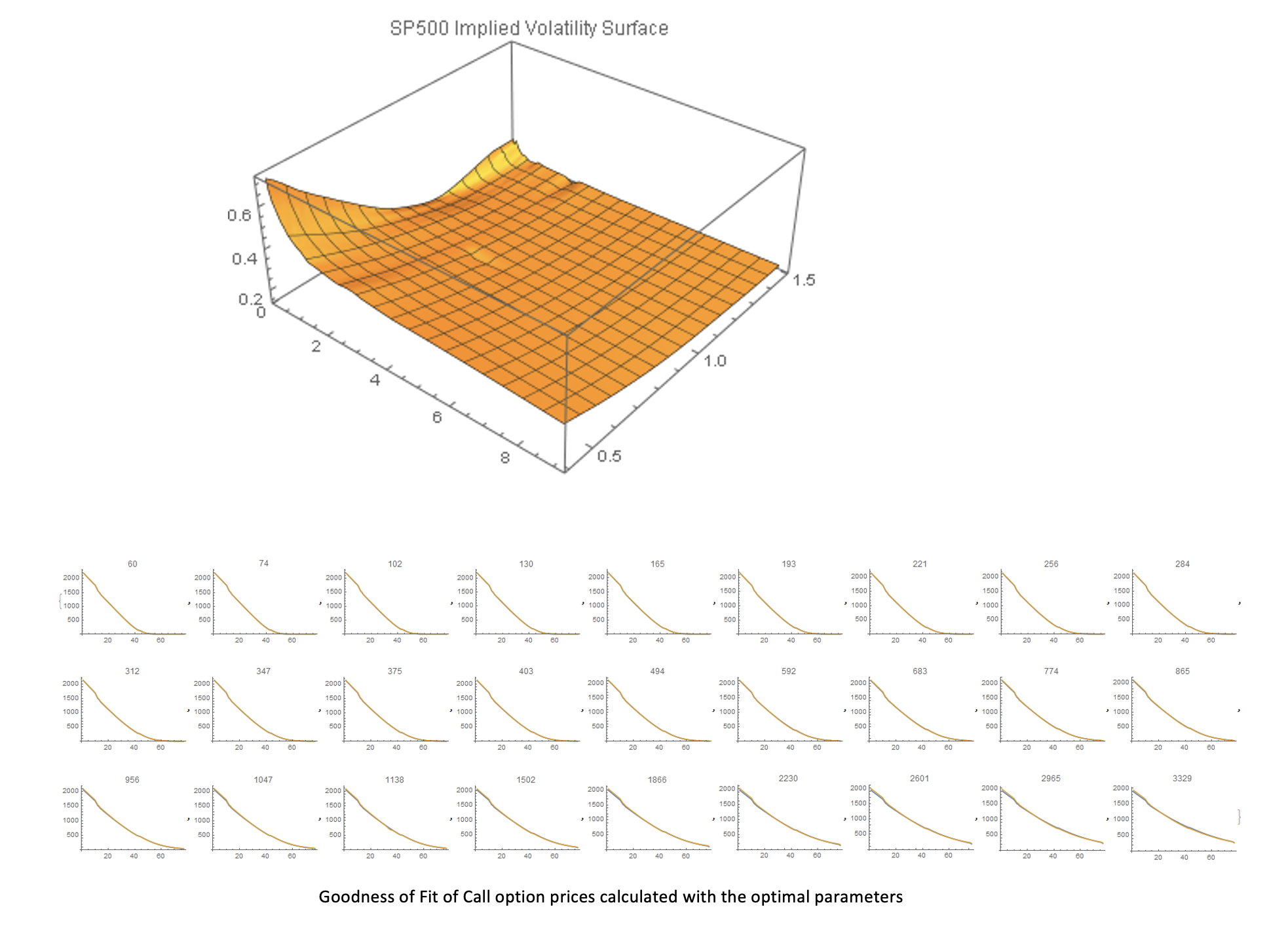
On the basis of market prices of a series of liquid vanilla options, we calibrate a Local Volatility option pricing model, which can be used to compute the prices of more complex exotic options.

Since in reality, the volatility varies for different strikes, the Black-Scholes model, where the volatility function is assumed to be constant for all maturities and strikes has been replaced by more sophisticated models which include local and stochastic volatility.

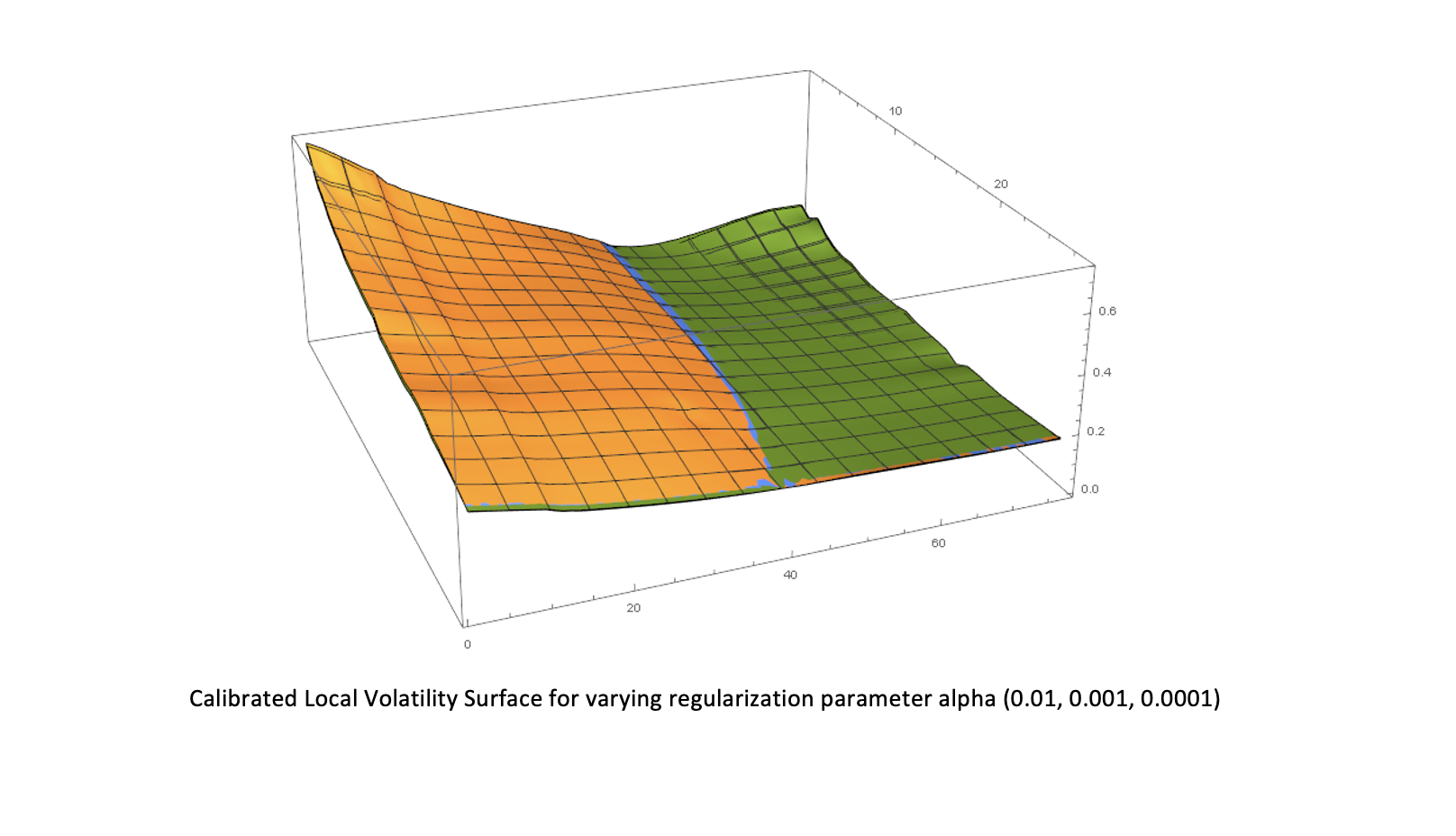
Determining the parameters of such a model in a way that the model prices of a set of options match the set observed market prices is the so-called calibration process. Mathematically this parameter identification is an ill-posed inverse problem and there may be several models with different parameters, which reproduce the quoted market prices in the same way. So the solution of the inverse problem needs not be unique, which leads to model uncertainty. Furthermore, the solution does not depend continuously on the input data. To overcome the ill-unconditionedness of the calibration problem, fast and stable algorithms have to be used. To guarantee stable parameters, the usage of regularization methods is essential.

We formulate the calibration problem as an optimization problem, where the goal is to fit the market prices as good as possible. The measure of the discrepancy between model prices and observed market prices is the sum of squared differences between them:

Mathematical formula for the objective function used in option pricing model calibration.

where S is the spot price of the underlying asset; K is the strike price of the option; T is the maturity of the option, w is the weight of the given option in cost function and t is the time at which the option is priced.

To solve the optimization problem classical gradient based methods can be used. To get the prices of the options for given parameters in the model, we have to solve a partial differential equation or use a Monte Carlo simulation. However, the objective function is not necessarily convex and so we cannot be sure that gradient based methods will not end up in a local minimum instead of the global one.

Dupire (1994) introduces the local volatility model, where the underlying price process is assumed to follow the stochastic process.

Stochastic differential equation representing the underlying asset's price process.

with a drift rate , a volatility function and the increment of a Wiener Process . The local volatility function cannot be overserved directly and has to be calibrated to a set of options as described above. Dupire showed that the local volatility function satisfies the formula.

Mathematical formula for local volatility used in the Dupire model.

It can be shown that for special implied volatility surfaces, the argument of the square root gets negative, and so a local volatility function cannot be observed.

If we assume the implied volatility to be high (70%) if the options are in or out of the money and low (20%) for ATM options, i.e..

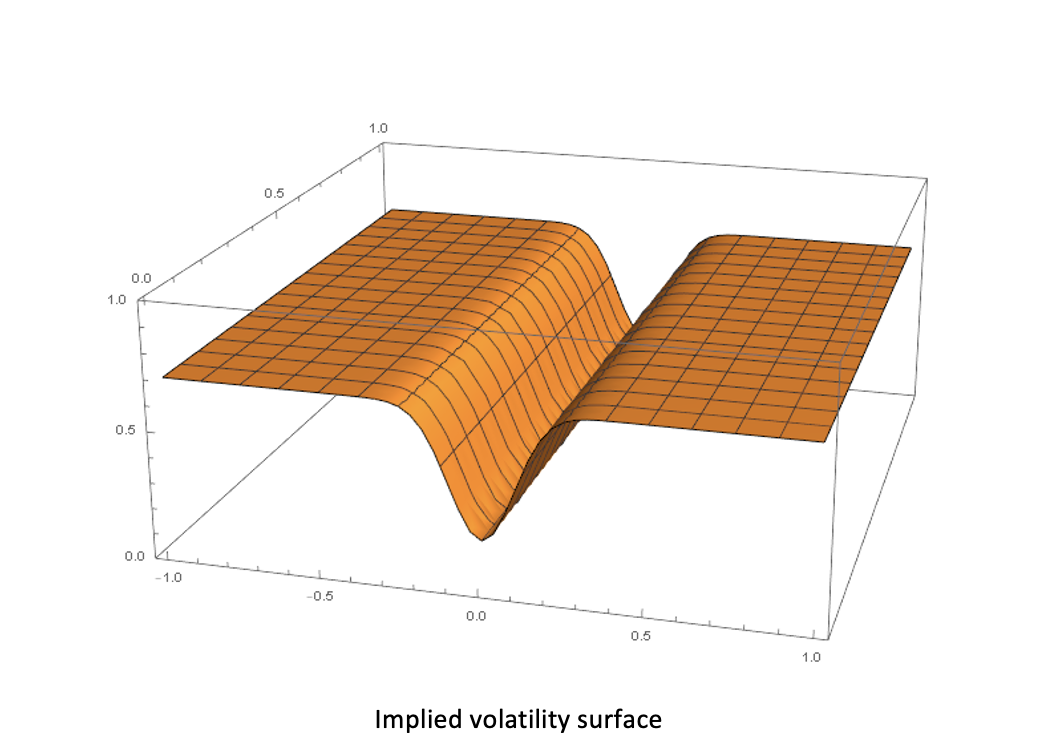
3D plot of an implied volatility surface.

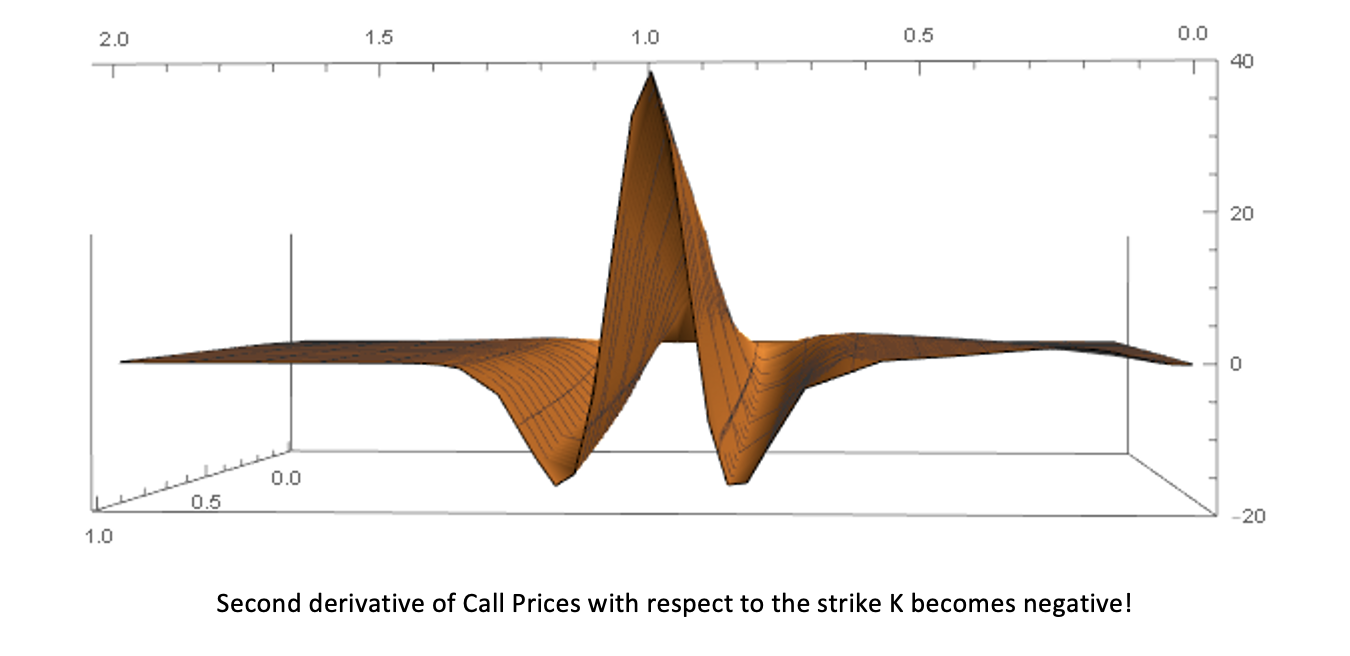
The market option prices, corresponding to the implied volatility surface above calculated by the Black Scholes formula have the following shape and the second derivative with respect to the strike K which is part of the local vola formula becomes negative which leads to the fact that the local volatility cannot be calculated for this setting.

3D plot of market prices of call options corresponding to the implied volatility surface.

We analyze the calibration routine of the Dupire model using S&P500 option data for a set of 27 maturities (from 1 month to 9 years) and 77 strikes (from 50% to 150% of the actual spot price).